John Conway’s cellular automaton, the Game of Life, has long been a staple project for those learning to code. It is also an “embarrassingly parallel” problem, making it a great learning tool for teaching ourselves how to parallelize processes using SYCL™. You will find that even the simplest parallel implementation of the Game of Life will yield a significant performance boost, however there are even more optimizations we can apply to squeeze as much performance out of our code. One such optimization is the use of local memory.

Key Concepts

Each thread in a SYCL kernel is referred to as a work-item. These work-items are arranged into work-groups. All work-items in all work-groups can access global memory, but frequent transactions with global memory can often incur overhead, particularly for a memory-bound problem such as this. Therefore, if we’re aiming for maximum optimization, we should avoid unnecessary global memory access. This is where local memory comes in. Alongside global memory, each work-item can access a region of high-bandwidth, low-latency local memory reserved for all items in its work-group. A work-item cannot access the local memory of another work-group. Local memory supplies a mechanism for us to minimize costly data transfer from global memory.

Consider a 48x48 Game of Life board comprising 2304 cells. In our kernel this will be mapped to nine 16x16 work-groups each consisting of 256 work-items. To determine whether a cell is alive or dead in the next iteration, our kernel needs to access the current cell and its 8 neighbours. If this kernel were to only use global memory, then each work-item would have to query global memory individually, 9 times. But we know that cells will share neighbours, so a lot of these global memory accesses are unnecessary. If we use local memory, each 8x8 work-group can copy the relevant chunk of global memory into local memory, creating a cache which allows us to read from global memory just once per work-item and then read from local memory instead.

Expressing our Kernel

You may already know that there are three different forms of parallel kernels in SYCL: basic data-parallel kernels, explicit ND-range kernels and hierarchical kernels. We can’t use a basic data-parallel kernel if we want to access local memory because basic kernels don’t index for local/group IDs. It is possible to use local memory in an ND-range kernel , however, we will be using a hierarchical kernel in this instance. This decision has been made for two reasons:

1. I believe that hierarchical kerne ls are a more intuitive way of visualizing and understanding how data transfer works under local memory
2. Hierarchical kernels automatically insert barriers between scopes, so we can worry less about data synchronization

A hierarchical kernel takes the general form of one or more parallel_for_work_item clauses enclosed within a parallel_for_work_group clause. Below is a skeleton of what our kernel should look like:

handler.parallel_for_work_group(numGroups, groupSize, [=](group<2> group) {
  // Initialize local memory
  group.parallel_for_work_item([&](h_item<2> item) {
    // Load data into local memory
  });
  // Compiler inserts implicit barrier here
  group.parallel_for_work_item([&](h_item<2> item) {
    // Perform computation
  });
});

Describing our Environment

The example project uses SDL2 to render the Game of Life, but you are free to use any framework capable of rendering 2D graphics. The current state (alive or dead) of each cell is stored in a one-dimensional array of Booleans called map. Our array must be one-dimensional because two-dimensional arrays aren’t stored contiguously in memory, however we can still index our array as if it were 2D by using a 2D buffer. MAPWIDTH and MAPHEIGHT are constants denoting the dimensions of the board. They must be multiples of the constant GROUPSIZE which is the side size of each work-group. There is no set way to determine the best work-group size for your processor , but a good starting point is to find the maximum work-group size using the following code:

sycl::device dev = myQueue.get_device();
std::cout << dev.get_info<sycl::info::device::max_work_group_size>();

Our kernel is defined within the function lifePass().

Data Flow

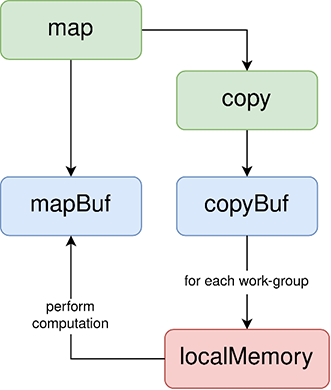
map is created in main and initialized with a random configuration of living and dead cells.

std::array <bool, MAPWIDTH * MAPHEIGHT> map;

With each call to lifePass(), a copy of map is created because we want to be able to write to map without having to worry about creating conflicts or data races between other work-items. Buffers also need to be created before we can submit our queue.

void lifePass() {
  std::array<bool, MAPWIDTH * MAPHEIGHT> copy = map;
  auto copyBuf = sycl::buffer<bool, 2>(copy.data(), sycl::range<2>{MAPWIDTH, MAPHEIGHT});
  copyBuf.set_final_data(nullptr);

  auto mapBuf = sycl::buffer<bool, 2>(map.data(), sycl::range<2>{MAPWIDTH, MAPHEIGHT});
  ...
}

When we submit our queue, we need to create accessors so that we can read from copy and write to map from within our kernel.

myQueue.submit([&](sycl::handler& cgh) {
  auto copyAcc = copyBuf.get_access<sycl::access::mode::read>(cgh);
  auto mapAcc = mapBuf.get_access<sycl::access::mode::write>(cgh);
  ...
}).wait();

Halo Regions

You may have realised that a potential complication with local memory usage are the cells at the edges of each work-group. We still need to access their neighbours, but they won’t be loaded into local memory. We address this by giving each tile of local memory a halo region. A halo region is a border of cells loaded into local memory alongside the cells which the work-group is actually operating on.

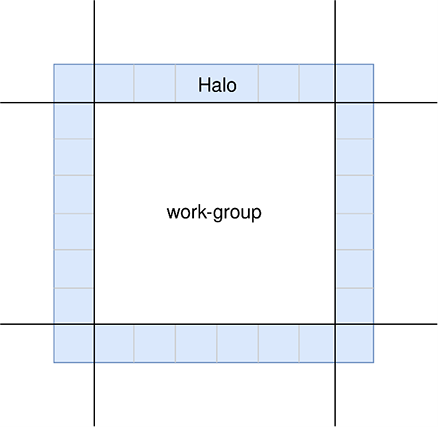
As the diagram above shows, for each load into local memory, we need to transfer the data for the work-group as well as the cells bordering that work-group's tile. We will only perform processing on the cells in the work-group as the halo cells will be handled in their own work-group – they are only there for us to access their contents as neighbouring cells. This means that the size of our local memory will be (GROUPSIZE + 2) * (GROUPSIZE + 2). We can now go ahead and initialize our local memory.

sycl::range<2> groupSize{GROUPSIZE + 2, GROUPSIZE + 2};
sycl::range<2> numGroups{((MAPWIDTH - 1) / GROUPSIZE) + 1, ((MAPWIDTH - 1) / GROUPSIZE) + 1};

cgh.parallel_for_work_group(numGroups, groupSize, [=](sycl::group<2> group) {
  bool localMemory[GROUPSIZE + 2][GROUPSIZE + 2] = 0;
  …
});

Defining localMemory at work-group scope means that it is in local memory. An important distinction to note is that our groupSize range takes the halo into account whereas numGroups is calculated without the halo.

Populating Local Memory

Now that each work-group has had its local memory initialized, data from copyAcc must be copied into local memory. This is performed within a parallel_for_work_item clause, meaning that each work-item will load its corresponding cell status into local memory in parallel. Consequently, once all work-items have reached the implicit barrier at the end of this kernel, local memory should be fully populated, ready for the next kernel to operate on.

group.parallel_for_work_item([&](sycl::h_item<2> item) {
  int localRow = item.get_local_id(0) ;
  int localCol = item.get_local_id(1);

  Sycl::id<2> groupId = group.get_group_id();

  int globalRow = (groupId[0] * GROUPSIZE) + localRow;
  int globalCol = (groupId[1] * GROUPSIZE) + localCol;

  if ( globalCol > MAPWIDTH || globalRow > MAPHEIGHT) {
    localMemory[localRow][localCol] = false;
  }
  else {
    localMemory[localRow][localCol] = copyAcc[globalRow – 1][globalCol – 1];
  }
});

For each work-item, this kernel is copying the state of the corresponding cell into local memory. localRow and localCol refer to the row and column of the current work-item within the work-group, whilst globalRow and globalCol index the current work-item in relation to the whole kernel. Ordinarily, we would get globalRow and globalCol by calling item.get_global_id(). However, because of our halo regions, get_global_id() will return an index which has been offset. Instead, the global indexes are calculated by finding the location of the top left corner of the work-group in the global space and then adding the local indexes to that. Before the data is copied, an if statement excludes any cells which are outside the map.

Let There be Life!

Now that local memory has been filled, we can carry out the logic which determines whether a given cell is alive or dead. This takes place in a separate parallel_for_work_item clause with an implicit barrier inserted before it to ensure that work does not begin until local memory is fully populated. The implementation of this is much the same as any other version of Life. The only difference is that our code is reading from local memory and thus indexing relative to the work-group range rather than the global range.

group.parallel_for_work_item([&](sycl::h_item<2> item) {
  int localRow = item.get_local_id(0);
  int localCol = item.get_local_id(1);

  sycl::id<2> groupId = group.get_group_id();

  int globalRow = (groupId[0] * GROUPSIZE) + localRow;
  int globalCol = (groupId[1] * GROUPSIZE) + localCol;

  if (localRow > 0 && localRow < (GROUPSIZE + 1) && localCol > 0 && localCol < (GROUPSIZE + 1)) {
      int liveNeighbourCount = 0;
      int neighbours[8] = {
      localMemory[localRow - 1][localCol - 1],
      localMemory[localRow - 1][localCol],
      localMemory[localRow - 1][localCol + 1],
      localMemory[localRow][localCol + 1],
      localMemory[localRow + 1][localCol + 1],
      localMemory[localRow + 1][localCol],
      localMemory[localRow + 1][localCol - 1],
      localMemory[localRow][localCol - 1]
    };
    for (auto neighbour : neighbours) {
      liveNeighbourCount += neighbour;
    }


    if ((localMemory[localRow][localCol]) && liveNeighbourCount < 2 || liveNeighbourCount > 3) {
      mapAcc[globalRow - 1][globalCol – 1] = false;
    }
    else if (liveNeighbourCount == 3) {
      mapAcc[globalRow - 1][globalCol – 1] = true;
    }
  }
});

We now have a working implementation of Conway’s Game of Life which makes use of local memory. Benchmarking on a board of size 100x100 compiling via DPC++ using the CUDA backend yields a kernel execution time of 27485 microseconds without local memory and 18159 microseconds with local memory. You can find the complete code here.

The next step for optimization would be to find any underlying communication patterns within work-groups and support them using sub-groups and collective functions. Feel free to experiment with the code and make your own modifications and enhancements.

Footnotes

[1] See this image convolution example: https://github.com/codeplaysoftware/syclacademy/blob/main/Code_Exercises/Exercise_18_Local_Memory_Tiling/solution.cpp

[2] See https://codeplay.com/portal/blogs/2020/01/09/sycl-performance-post-choosing-a-good-work-group-size-for-sycl.html for an extensive guide to determining work-group sizes