Ray-tracing in a Weekend with SYCL Part 2: Pixel sampling and Material tracing
19 June 2020
This post follows on from the first part of my blog, where I showed how the I adapted the code from "Ray Tracing in one weekend" to increase performance using SYCL™. The first area I tackled was the rendering. If you haven't read it already, it's on our blog here.
In this second post I'll show how to use SYCL to improve the performance of this code further using some interesting techniques.
Pixel sampling (Anti-aliasing)
As described in the Raytracing in a Weekend book, to implement anti-aliasing we will do what is called "super sampling." Super sampling works by taking N samples for each pixel, from random parts of that pixel, and averaging the result. The more samples you take, the closer you get to the ideal "alias free" image. That being said, we need a way of working with random numbers on the device, which will require keeping a random state for each work-item in a work-group.
Let's implement a simple device random number generator in SYCL to do this. We can use a variation of a Xorshift random number generator and initialize its state by giving it a seed on the device side. For that we need a state structure and a fairly good integer hashing function.
Based on that information, we can now implement a simple version of a variation of the xorshift random generator - xorwow (based on the approach of AMD®'s rocRAND library, but simplified).
Implementing a random generator for use on the device
We implement a 32 bit unsigned int hashing so our generator will be storing its state as uint32_t
values, meaning we can just abstract the concrete typing away by using an alias - using
int_type = uint32_t. Here is the definition of the xorwow state.
struct xorwow_state_t {
// xorshift values (160 bits)
int_type x;
int_type y;
int_type z;
int_type w;
int_type v;
// sequence value
int_type d;
};
And the following is a standard implementation of the xorwow algorithm.
inline int_type xorwow(xorwow_state_t* state) {
int_type t = (state->x ^ (state->x >> 2));
state->x = state->y;
state->y = state->z;
state->z = state->w;
state->v = (state->v ^ (state->v << 4)) ^ (t ^ (t << 1));
state->d = state->d + 362437;
return state->v + state->d;
}
Now we need to be able to seed our generator by hashing the state.
template
inline xorwow_state_t get_initial_xorwow_state(int_type seed) {
xorwow_state_t state;
state.d = !seed ? 4294967295 : seed;
for (auto i = 0; i < num_iters; i++) {
state.x = hash(state.d);
state.y = hash(state.x);
state.z = hash(state.y);
state.w = hash(state.z);
state.v = hash(state.w);
state.d = hash(state.v);
}
return state;
}
As you can see it's possible to tweak the number of iterations depending on how good you want your hashed state to be. I found 8 to be enough for the purpose of this ray tracer. Additionally, the hash function that I am using is the Mueller hash. There is a very descriptive topic on StackOverflow about good integer hash functions for random number generators which you can have a look at if you are interested.
Here is the mueller_hash function.
inline int_type mueller_hash(int_type x) {
x = ((x >> 16) ^ x) * 0x45d9f3b;
x = ((x >> 16) ^ x) * 0x45d9f3b;
x = ((x >> 16) ^ x);
return x;
}
If you want to test out multiple hash functions you can define a macro to make this easier, for
example I used - #define hash(x) (mueller_hash(x)).
Now that we have our random number generator set up, we need to convert the generated numbers to uniform values, since this is what we need to pass in our vec3 to do the tracing computation. Assuming that our real (floating point) type is single precision float, we can convert the integer values to a uniform with this trick.
template <class rng_t, class state_t, typename data_t = float>
inline data_t rand_uniform(rng_t rng, state_t* state) {
auto a = rng(state) >> 9;
auto res = data_t{0.0};
*(reinterpret_cast<int_type*>(&res)) = a | 0x3F800000;
return res - data_t{1.0};
}
The template arguments rng_t and state_t are there so that we can define rand_uniform as a meta function for uniform sampling that can accept various generators, and their corresponding states, in case you want a different random generator and/or state for your ray tracer.
Adding sampling to the render kernel using the random generator
We have done all the preparation so that we can now continue and introduce device-side random numbers in our ray-tracer in order to implement sampling.
Initializing the state of the random generator on the device:
Firstly, we need to initialize the random generator's state on the device, therefore we need to
introduce a new kernel that we will call render_init_kernel and this will be called right
before render_kernel.
template <int width, int height>
class render_init_kernel {
template <typename data_t>
using write_accessor_t = sycl::accessor<data_t, 1, sycl::access::mode::write,
sycl::access::target::global_buffer>;
public:
render_init_kernel(write_accessor_t<state_t> rand_states_ptr)
: m_rand_state_ptr(rand_states_ptr) {}
void operator()(sycl::nd_item<2> item) {
const auto x_coord = item.get_global_id(0);
const auto y_coord = item.get_global_id(1);
const auto pixel_index = y_coord * width + x_coord;
const auto state = get_initial_xorwow_state(pixel_index);
m_rand_states_ptr[pixel_index] = state;
}
private:
write_accessor_t<xorwow_state_t> m_rand_states_ptr;
};
Implementing sampling using the random generator in the render kernel
All of the work we have done until now was so that we can use our random generator inside the render kernel and now we can finally do that. The following code snippet demonstrates how we use the random number generator to introduce pixel sampling (anti-aliasing) when calculating the final color value.
void operator()(sycl::nd_item<2> item) {
[...]
// initialize local (for the current thread) random state
auto local_rand_state = m_rand_state_ptr[pixel_index];
// create a 'rng' function object using a lambda
auto rng = [](xorwow_state_t* state) { return xorwow(state); };
// capture the rand generator state -> return a uniform value
auto randf = [&local_rand_state, rng]() { return rand_uniform(rng, &local_rand_state); };
// color sampling
vec3 final_color(0.0, 0.0, 0.0);
for (auto i = 0; i < samples; i++) {
const auto u = (x_coord + randf()) / static_cast<real_t>(width);
const auto v = (y_coord + randf()) / static_cast<real_t>(height);
ray r = m_camera_ptr.get_pointer()->get_ray(u, v, rng, &local_rand_state);
final_color += color(r, m_spheres_ptr, rng, &local_rand_state, max_depth);
}
final_color /= static_cast<real_t>(samples);
// apply gamma correction
final_color.x = sycl::sqrt(final_color.x);
final_color.y = sycl::sqrt(final_color.y);
final_color.z = sycl::sqrt(final_color.z);
// store final color
m_frame_ptr[pixel_index] = final_color;
}
As you can see it becomes quite trivial to use the random number generator in kernel code after we have set it up. Instead of using lambdas, you can define function objects that will be re-usable but in this case we only need it for the render kernel so I've gone forward with lambdas.
You can see that we also introduce a camera accessor here (m_camera_ptr). It is now possible to
initialize the camera on the device. Our "device" is the target processor for parallel execution, for
example a GPU. The camera is required because later the author introduces some operations in the
get_ray function that are part of the camera that require use of the random generator. Access to the
camera is read-only, thus, all you have left to do is add an accessor member in the render_kernel class
and initialize it in the constructor. Then you will be able to create a ray using the camera class as
seen in the kernel code above. The camera implementation is identical to that in the the book so you
can have a look there at Chapter 6 or in the source code repository of the book.
Calling the new render_init and render kernels
We will abstract the execution of this kernel in a separate function that sets up the device buffers and launches the kernel in parallel. It is similar to how we defined the render function in the first blog post.
template <int width, int height>
void render_init(sycl::queue& queue, xorwow_state_t* rand_states) {
constexpr auto num_pixels = width * height;
// allocate memory on device
auto rand_states_buf = sycl::buffer<xorwow_state_t, 1>(rand_states, sycl::range<1>(num_pixels));
// submit command group on device
queue.submit([&](sycl::handler& cgh) {
// get memory access
auto rand_states_ptr = rand_states_buf.get_access<sycl::access::mode::write>(cgh);
// setup kernel index space
const auto global = sycl::range<2>(width, height);
const auto local = sycl::range<2>(tileX, tileY);
const auto index_space = sycl::nd_range<2>(sycl::range<2>(width, height), sycl::range<2>(tileX, tileY));
// construct kernel functor
auto render_init_func = kernels::render_init_kernel<width, height>(rand_states_ptr);
// execute kernel
cgh.parallel_for(index_space, render_init_func);
});
}
Then, from the main entry point on the host, we simply create an array of random states that equals the number of pixels we will be coloring.
std::vector<xorwow_state_t> rand_states(num_pixels);
render_init<width, height>(queue, rand_states.data());
Now we have to modify the render function that launches our render kernel to compute the tracing. We need to initialize the random states buffer in the render function so that we can pass it to the kernel function object, and use it to carry out the computations that require random number generation.
template <int width, int height, int samples, int num_spheres>
void render(sycl::queue& queue, vec3* fb_data, sphere* spheres, camera* cam, xorwow_state_t* rand_states) {
constexpr auto num_pixels = width * height;
// allocate memory on device
sycl::buffer<vec3, 1> frame_buf(fb_data, sycl::range<1>(num_pixels));
sycl::buffer<sphere, 1> spheres_buf(spheres, sycl::range<1>(num_spheres));
sycl::buffer<camera, 1> camera_buf(cam, sycl::range<1>(1));
sycl::buffer<xorwow_state_t, 1> rand_states_buf(rand_states, sycl::range<1>(num_pixels));
// submit command group on device
queue.submit([&](sycl::handler& cgh) {
// get memory access
auto frame_ptr = frame_buf.get_access<sycl::access::mode::write>(cgh);
auto spheres_ptr = spheres_buf.get_access<sycl::access::mode::read>(cgh);
auto camera_ptr = camera_buf.get_access<sycl::access::mode::read>(cgh);
auto rand_states_ptr = rand_state_buf.get_access<sycl::access::mode::read_write>(cgh);
// setup kernel index space
const auto global = sycl::range<2>(width, height);
const auto local = sycl::range<2>(tileX, tileY);
const auto index_space = sycl::nd_range<2>(global, local);
// construct kernel functor
auto render_func = kernels::render_kernel<width, height, samples, num_spheres>(frame_ptr, spheres_ptr, camera_ptr, rand_states_ptr));
cgh.parallel_for(index_space, render_func);
});
}
For readability purposes I am keeping buffer initializations inside the render_init and render kernels, however, it is better to create the buffers that both kernels depend on outside of the local scope of each the individual functions that run the kernels. This means you can keep those buffers alive for as long as needed, and avoid unnecessary device allocation and de-allocation calls for per iteration. This will benefit the run-time performance because less memory operations are performed and this ultimately improves the memory throughput. Here is the host setup in main() where we call the render function with two new arguments - camera and random states.
vec3 look_from(-2.0f, 2.0f, 1.0f);
vec3 look_at(0.0f, 0.0f, -1.0f);
vec3 up(0.0f, 1.0f, 0.0f);
float angle = 90.0f;
camera cam(look_from, look_at, up, angle, static_cast<real_t>(width) / static_cast<real_t>(height));
render<width, height, samples, num_spheres>(queue, fb.data(), spheres.data(), &cam, rand_state.data());
You may be thinking whether this is the only way to generate pseudo-random numbers on the device side with SYCL. The SYCL Pseudo Random Number Generator project, created by the Wigner Research Lab shows an alternative. The project aims to implement various standard layout pseudo random number generators that can be used with SYCL. The library is currently in alpha version but is usable and the authors have included various useful examples.
Material Tracing
We are now at the stage of finally adding some diffuse shading to the rendered spheres. This means implementing Lambert’s cosine law but we are not going to introduce a new structure at this point, rather we will transform our color function directly.
Material Instances will be slightly trickier to get up and running on the device with our current architecture, thus they will be covered after adding the diffuse shading which will be required to modify the implementation our color() function inside render_kernel.
Diffuse shading in the reference implementation - Recursive approach
The original implementation from the book uses recursion to send enough rays to approximate the Lambertian shading model. So here is the actual code we've got for coloring. We don't use recursion as this is not possible inside SYCL kernels.
template <class rng_t>
vec3 color(const ray& r, const sycl::global_ptr<sphere>& spheres,
rng_t rng, xorwow_state_t* local_rand_state) {
static const auto max_real = std::numeric_limits<real_t>::max();
hit_record rec;
if (spheres->hit(r, real_t{0.001}, max_real, rec)) {
vec3 target = rec.p + rec.normal + random_in_unit_sphere(rng, local_rand_state);
return 0.5 * color(ray(rec.p, target-rec.p), world);
}
else {
vec3 unit_direction = unit_vector(r.direction());
float t = 0.5 * (unit_direction.y() + 1.0);
return (1.0 - t) * vec3(1.0, 1.0, 1.0) + t * vec3(0.5, 0.7, 1.0);
}
}
Fundamentally, not all GPUs can support recursive function calls, but even if they could, they will most-likely be quite slow and introduce other limitations due to a very small stack depth. Therefore, the default translation of the color function the way it is written in the original code will result in a stack overflow since it calls itself too many times.
Diffuse Shading on the GPU - Iterative approach
The work around to our problem is straightforward - turning the recursion into a standard iteration using for loop. We can do that by setting a number of 50 iterations since the author limits the recursion to that many calls in a later chapter of the book anyway.
template <class rng_t>
vec3 color(const ray& r, const sycl::global_ptr<sphere>& spheres,
rng_t rng, xorwow_state_t* local_rand_state, int depth) {
static const auto max_real = std::numeric_limits<real_t>::max();
ray cur_ray = r;
vec3 cur_attenuation(1.0, 1.0, 1.0);
for (auto i = 0; i < depth; i++) {
hit_record rec;
if (hit_world(cur_ray, real_t{0.001}, real_max, rec, spheres)) {
vec3 target = rec.p + rec.normal + random_in_unit_sphere(rng, local_rand_state);
cur_attenuation *= 0.5;
cur_ray = ray(rec.p, target-rec.p);
}
else {
vec3 unit_direction = unit_vector(cur_ray.direction());
float t = 0.5 *(unit_direction.y() + 1.0);
vec3 c = (1.0 - t) * vec3(1.0, 1.0, 1.0) + t * vec3(0.5, 0.7, 1.0);
return cur_attenuation * c;
}
}
// exceeded recursion ...
return vec3(0.0, 0.0, 0.0);
}
Finally, you can setup the spheres on the host side by having a look at the values used in the Raytracing in a Weekend chapter where the author adds diffuse material.
Produces:

This next section aims to show how to create polymorphic geometry in SYCL, before jumping into the implementation for materials and tying them to the specific geometry class.
Polymorphic geometry types - Device-side polymorphism
Back in the first blog where I introduced simple sphere tracing with SYCL, I have simplified the original implementation of the application by not using polymorphism since we only work with spheres. However, the reference C++ implementation has the sphere class inherit from a base interface named hitable. In order to enable the flexibility of the ray-tracer so it could work with other geometries we have to add this polymorphic behavior.
The issue we are faced with here is the limitation of using traditional dynamic (or run-time) polymorphism inside SYCL kernels.
Fortunately, with C++ we can emulate this using techniques for achieving polymorphism at compile-time.
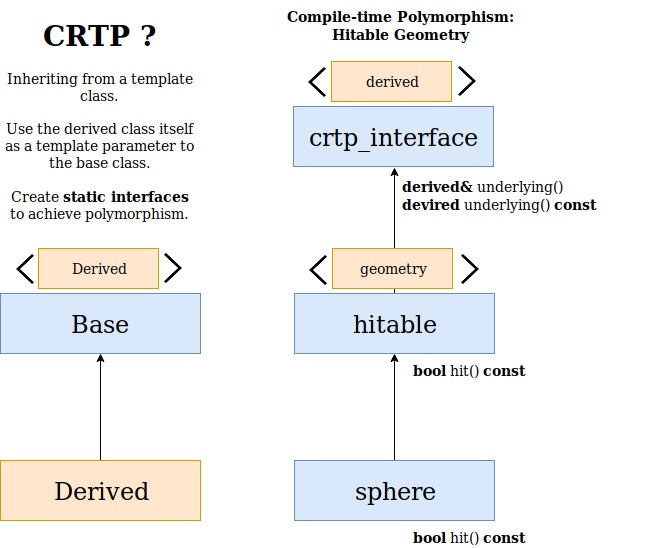
The diagram above presents a polymorphic class hierarchy using a C++ design pattern called CRTP (Curiously Recurring Template Pattern). On the left side is visible a general overview of the pattern while on the right side is the structure we will introduce into this application.
With CRTP we can have static polymorphism, thus all calls to the overloaded function of the bases interface will be resolved at compile-time. This is one possible work-around to the said limitation. There is a blog post that provides more detail on the use of CRTP with SYCL if you are interested in more context.
Polymorphic geometry rendering
Now changes to the render_kernel and render function are as trivial as passing the hitable type appropriately.
Non-generic render kernelWhat we used to have was an implementation that was tied to buffers objects that wrap explicitly over the sphere type and accessor objects to those sphere buffers. This works fine because we only implement spheres anyway, but our goal was to optimize the ray tracer without trading functionality for performance, such as losing the ability to use generic geometry types.
template <int width, int height, int samples, int max_depth, int num_spheres>
class render_kernel {
public:
render_kernel(write_accessor_t<vec3> frame_ptr,
read_accessor_t<sphere> spheres_ptr,
read_accessor_t<camera> camera_ptr,
read_accessor_t<xorwow_state_t> rand_state_ptr)
: m_frame_ptr(frame_ptr),
m_spheres_ptr(spheres_ptr),
m_camera_ptr(camera_ptr),
m_rand_state_ptr(rand_state_ptr) {}
[...]
};
Here is some code showing how we apply CRTP in C++ to work for our polymorphic hierarchy of classes that inherit from hitable.
template <class geometry>
class hitable {
public:
bool hit(const ray& r, real_t t_min, real_t t_max, hit_record& rec) const {
return static_cast<const derived&>(*this).hit(r, t_min, t_max, rec);
}
};
class sphere : public hitable<sphere> {
public:
sphere() = default;
bool hit(const ray& r, real_t t_min, real_t t_max, hit_record& rec) const {
[...]
}
};
Essentially what is happening is that the base class hitable is designed to be inherited from its template parameter, and by nothing else. Therefore, it takes this as an assumption, and a static_cast is enough to get the derived type.
Additionally, we can factor out the static_cast calls by forwarding the underlying type to a higher hierarchy level which we call the crtp::interface.
template <class derived>
struct crtp {
derived& underlying() { return static_cast<derived&>(*this); }
const derived& underlying() const {
return static_cast<const derived&>(*this);
}
};
template <class geometry>
class hitable : crtp<geometry> {
public:
bool hit(const ray& r, real_t min, real_t max, hit_record& rec) const {
return this->underlying().hit(r, min, max, rec);
}
};
class sphere : public hitable<sphere> {
[...]
};
This way we are not only abstracting the access to the underlying type, but also dealing with both cases where the underlying object is a non-const and const. We are now using this ? underlying() to access the function implementation in the derived class because names in template base classes get ignored.
Generic render kernel
However, we can now template the render_kernel function object over the type of the hitable.
template <int width, int height, int samples, int max_depth, int num_spheres, class hitable>
class render_kernel {
public:
render_kernel(write_accessor_t<vec3> frame_ptr,
read_accessor_t<hitable> hitables_ptr,
read_accessor_t<camera> camera_ptr,
read_accessor_t<xorwow_state_t> rand_state_ptr)
: m_frame_ptr(frame_ptr),
m_spheres_ptr(spheres_ptr),
m_camera_ptr(camera_ptr),
m_rand_state_ptr(rand_state_ptr) {}
[...]
};
The render function is templated similarly. This where we previously created
sycl::buffer<sphere> and now it is going to be whatever type has been deduced from the
hitable template parameter.
template <int width, int height, int samples, int max_depth, int num_hitables,
class hitable>
void render(sycl::queue& queue, vec3* fb_data, hitable* hitables, camera* cam,
xorwow_state_t* rand_state_data) {
[...]
}
Evaluating multiple material types
There are two options to go about materials in geometries, and one is to have their properties tightly coupled with the geometry where we add all of the various material properties as class members to each geometry class, or detach them (abstract) in a separate class for each material type.
As we follow the Raytacing in one Weekend, we can see that there are three material types implemented for the ray tracer. They are polymorphic, so there is a base class Material and the derived ones are called Lambertian, Metal and Dielectric.
So the reference implementation from the book, being traditionally object-oriented, has a component of Material class in the Sphere class. However, this can be problematic in SYCL code as we cannot nest pointers in device memory.
Here is how the class definition will look.
class geometry {
public:
geometry() {}
bool hit(...) const { return [...] }
private:
material* m_material;
};
Here material is an interface and is evaluated through the use of dynamic polymorphism. We did learn about how to achieve static polymorphism in SYCL, and it is possible as we know the material types beforehand too, but the problem is the introduction of this pointer nesting.
We can't have a SYCL buffer for our geometry defined as before (sycl::buffer<geometry> geom_buf) because of the underlying pointer for material. In theory we could try and argue about allocating the material data on the device as well, but this particular case is deliberately omitted in the SYCL specification due to the fact that there is no guarantee that the material pointers are persistent in device memory. In other words, this is referred to as pointer chasing which is not allowed and strongly not recommended on the device side. Also, such functionality is not currently part of the SYCL specification or any of the implementations. Therefore, implementing the evaluation for multiple material types will require us to re-visit the design.
A possible solution is to have a tighter relation between the material properties and the geometry, which is the simplest approach that will be discussed in this section. To achieve this we also need to modify the hit_record structure in a similar way to the geometry so that it holds the material properties separately, and get rid of the raw pointer to material.
Now before getting into implementation details, let's list the properties of each of the materials that are part of the book.
Lambertian (diffuse material)- albedo - the proportion of incident light that is reflected away from a surface. Essentially, it calculates the attenuation; the lower it is the darker the material color, and the higher it is the brighter the object.
- fuzz - manages the blurriness of the reflection, clamped between 0 and 1. It is applied to the random point (normalized position) in a geometry.
- refractive index - used in Snell’s Law, to calculate total reflection. Dielectric material can reflect light and at the same time let the light pass through - refract.
In order to keep track of the material type upon intersection, we will use enumeration for each type. This entire approach assumes we do know the types beforehand because we will implement the evaluation in such a way that it depends on that knowledge.
s// supported material types
enum class material_t { Lambertian, Metal, Dielectric };
Accordingly, the hit_record struct (as well as the sphere class) will have to store all of the possible material properties as opposed to having a pointer to the material interface which types are deduced at run-time. Another change here is that the material evaluation is now done in hit_record.
class hit_record {
public:
hit_record() = default;
template <class rng_t>
bool scatter_material(const ray& r_in, const hit_record& rec,
vec3& attenuation, ray& scattered,
rng_t rng, xorwow_state_t* local_rand_state);
vec3 center;
real_t radius;
// material properties
material_t material_type;
vec3 albedo;
real_t fuzz;
real_t refraction_index;
}
Here is how the evaluation in scatter_material is implemented for each material type - by using a switch statement we provide the correct behaviour for the selected material_type value.
template <class rng_t>
bool scatter_material(const ray& r_in, const hit_record& rec,
vec3& attenuation, ray& scattered,
rng_t rng, xorwow_state_t* local_rand_state) {
switch (material_type) {
case material_t::Lambertian:
{
// evaluate the lambertian material type
[...]
}
case material_t::Metal:
{
// evaluate the metal material type
[...]
}
case material_t::Dielectric:
{
// evaluate the dielectric material type
[...]
}
default:
/* cannot reach here since a material must be defined
* when upon initialization of a geometry (sphere). */
return false;
}
}
Futhermore, this approach will require us to add multiple constructors to the sphere class due to the fact that metals and dielectrics introduce additional properties that are setup on instantiation of a sphere object.
Below is the definition of each constructor.
class sphere : public hitable<sphere> {
public:
sphere() = default;
/**
* Constructor for a sphere object with lambertian material
**/
sphere(const vec3& cen, real_t r, material_t mat_type, const vec3& color) :
center(cen), radius(r), material_type(mat_type), albedo(color)
{ }
/**
* Constructor for a sphere object with metal material
**/
sphere(const vec3& cen, real_t r, material_t mat_type, const vec3& mat_color, real_t f) :
center(cen), radius(r), material_type(mat_type), albedo(color), fuzz(clamp(f, 0.0, 1.0)
{ }
/**
* Constructor for a sphere object with dielectric material
**/
sphere(const vec3& cen, real_t r, material_t mat_type, real_t ref_idx) :
center(cen), radius(r), material_type(mat_type), refraction_index(ref_idx)
{ }
bool hit(const ray& r, real_t t_min, real_t t_max, hit_record& rec) const {
return [...]
}
// material properties
material_t material_type;
vec3 albedo;
real_t fuzz;
real_t refraction_index;
};
Now that this is taken care of, the color function needs to be modified so that the material evaluation does not happen through sphere?material?scatter but via the intersection information stored in hit_record (in function color : if (rec.scatter_material(...)) { ... }).
Finally, when we instantiate the spheres, one large one with lambertian material for the ground and three smaller ones in the center with the three material types (lambertian, metal, dielectric), we can see that they are correctly evaluated in the render kernel.

Some Optimization Improvements
The described approach is neither the most performant, nor the cleanest design-wise, but it demonstrates a way to integrate SYCL for a more special case which exists in many C++ object-oriented code bases. There are more optimal ways of evaluating the materials, such as keeping the implementations in a separate class for each material type.
Here is an overview of the major design changes towards such optimization:
- Store the materials in SYCL buffers separate from the corresponding geometry class
- SIndex into them via some int values that will be the material Id
This approach will benefit both performance and memory bandwidth because we won't be passing large geometry objects around, and the device can focus more on the computations.
Rendering the final scene
We are finally at the stage where we can render that final scene from the book and enjoy the much faster rendering of our SYCL ray tracer.
We can use two approaches:
- Create the world by initializing all geometry (random spheres in this case) on the host by using a host-side random generator and then render it on the device
- Utilize the device to create all of the random spheres by using our device-side random generator for this purpose.
The random spheres scene defined in the ray-tracing in a weekend book:
- 1 large sphere - lambertian - used to simulate a feeling for having an actual ground.
- 3 big spheres - lambertian, metal, dielectric in the middle to better showcase the reflections and refractions.
- 22 * 22 smaller spheres with randomly selected material and position properties.
Creating the world on the host
We can make use of an even simpler random uniform number generator (a variation based on xorshift) for quick and easy use on the host side.
template <typename data_t>
inline data_t xorand() {
union {
int_type ui;
data_t uf;
} result{};
auto fmask = (1u << 23u) - 1u;
result.ui = (rand() & fmask) | 0x3f800000u;
return result.uf - data_t{1.0};
};
And now we can proceed by creating the random scene from the book. To do this, we just need to add the world creation logic inside the application main() before initializing the renderer via the initialization kernel.
// define material types
auto lambertian = material_t::LAMBERTIAN;
auto metal = material_t::METAL;
auto dielectric = material_t::DIELECTRIC;
// define random generator
auto randf = [] { return xorand<real_t>(); };
// lambda to define the logic for random world generation
auto create_world = [&spheres, lambertian, metal, dielectric, randf]() {
spheres.push_back(sphere(vec3(0.0f, -1000.0f, -1.0f), 1000.0f, lambertian, vec3(0.5f, 0.5f, 0.5f)));
for (auto i = -11; i < 11; i++) {
for (auto j = -11; j < 11; j++) {
const auto choose_mat = randf();
vec3 center(i + randf(), 0.2f, j + randf());
if (choose_mat < 0.8f) { /// chosen lambertian
spheres.push_back(sphere(center, 0.2, lambertian,vec3(randf(), randf(), randf())));
} else if (choose_mat < 0.95f) { /// chosen metal
spheres.push_back(sphere(center, 0.2f, metal, vec3(0.5f * (1.0f + randf()),
0.5f * (1.0f + randf()), 0.5f * (1.0f + randf())), 0.5f * randf()));
} else { /// chosen dielectric
spheres.push_back(sphere(center, 0.2f, dielectric, 1.5f));
}
}
}
spheres.push_back(sphere(vec3(0.0, 1.0, 0.0), 1.0, dielectric, 1.5));
spheres.push_back(sphere(vec3(-4.0, 1.0, 0.0), 1.0, lambertian, vec3(0.4, 0.2, 0.1)));
spheres.push_back(sphere(vec3(4.0, 1.0, 0.0), 1.0, metal, vec3(0.7f, 0.6, 0.5), 0.0));
};
Creating the world on the device
Another possibility is to initialize the world on the SYCL device instead of on the host, giving us more flexibility to re-use the already allocated device memory.
template <int num_spheres, class hitable>
class create_world_kernel {
public:
create_world_kernel(write_accessor_t<hitable> spheres_ptr,
read_accessor_t<xorwow_state_t> rand_state_ptr)
: m_spheres_ptr(spheres_ptr), m_rand_state_ptr(rand_state_ptr) { }
void operator()(sycl::nd_item<1> item);
private:
write_accessor_t<hitable> m_spheres_ptr;
read_accessor_t<xorwow_state_t> m_rand_state_ptr;
};
We can use the device side specialized random generator and initialize just a single state. This is unlike the render initialization kernel where we define a state for each pixel, because here all the work will be done in the first allocated thread.
void operator()(sycl::nd_item<1> item) {
const auto local_id = item.get_local_id(0); // thread id
const auto group_id = item.get_group(0); // block id
if (local_id == 0 && group_id == 0) {
const auto global_id = item.get_global_id(0);
/* 1. Setup the random number generator */
// seed the random generator
m_rand_state_ptr[global_id] = get_initial_xorwow_state(global_id);
// initialize local (for the current thread) random state
auto local_rand_state = m_rand_state_ptr[global_id];
// create a 'rng' function object -> return random generated number
auto rng = [](state_t* state) { return xorwow(state); };
// capture the rand gen state -> return a uniform value.
auto randf = [&local_rand_state, rng]() {
return rand_uniform(rng, &local_rand_state);
};
// capture the uniform rand lambda -> return a vec3 with uniform values
auto rand_vec3f = [randf]() { return vec3(randf(), randf(), randf()); };
/* 2. define material types (identical to the host version) */
/* 3. initialize the sphere objects in the nested for loops
}
}
The branching involved in this can affect the GPU performance worse than expected, as opposed to doing it on the host where the CPU will have no issues with the if-else conditional logic, so depending on the selected SYCL device for running the application you can determine your choice. This approach can come in handy if you wish to have the geometry on the device from the beginning of the application, may be re-use the buffers for other computations before getting to rendering.

In this blog series I've tried to give some practical advice on how to take an existing application and optimize its performance using SYCL. By initially profiling the execution of the application I was able to pinpoint which parts of the application were taking the most time to execute, and was able to optimize some of these so that they could be run in parallel on a device such as a GPU. I hope it has been helpful and if you want to discuss any parts further why not start a thread on our forum? Visit our developer website to access the forum.
